Bạn có việc về hệ thức lượng vào tam giác nhưng bạn lại không biết phương pháp làm như thế nào bởi bạn không lắm được kiến thức. Cũng chính vì vậy, bài viết này trung học phổ thông Chuyên Lam tô muốn chia sẻ đến chúng ta hệ thức lượng vào tam giác vuông, cân, thường các bạn cần học tập thuộc để áp dụng vào giải bài xích tập.
Bạn đang xem: Hệ thức lượng trong tam giác thường
Hệ thức lượng giác vào tam giác vuông
Các hệ thức lượng trong tam giác thường
Các dạng bài tập hệ thức trong tam giác gồm lời giải
Hệ thức lượng giác trong tam giác vuông
Cho tam giác ABC vuông góc trên đỉnh A (Aˆ = 90º), ta có:b² = a.b’; c² = a.c’Định lý Pitago: a² = b² + c²a.h = b.ch² = b’.c’¹⁄h² = ¹⁄b² + ¹⁄c²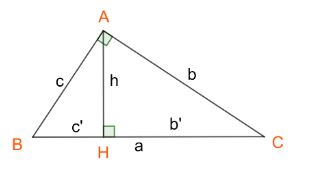
1. Tỉ số lượng giác của góc nhọn
a. Định nghĩa
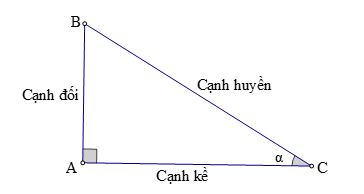
Hay sinα = AB/BC; cosα = AC/BC; tanα = AB/AC; cotα = AC/AB.
Nhận xét: nếu như α là một trong góc nhọn thì 0 0; cotα > 0
b. Định lý:
Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Tức là: đến hai góc α, β tất cả α + β = 90°
Khi đó: sinα = cosβ; cosα = sinβ; tanα = cotβ; cotα = tanβ.
c. Một số hệ thức cơ bản
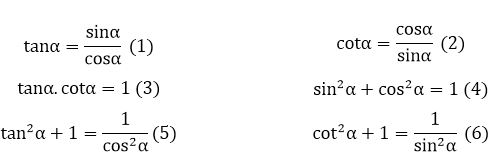
d. So sánh các tỉ số lượng giác
1. đến α, β là nhị góc nhọn. Giả dụ α sinα cosα > cosβ; cotα > cotβ
2. Sinα sinx = cos (90° – x)Cosx = sin (90° – x)tanx = cot (90° – x)cotx = tung (90° – x)
2. Hệ thức về góc và cạnh trong tam giác vuông
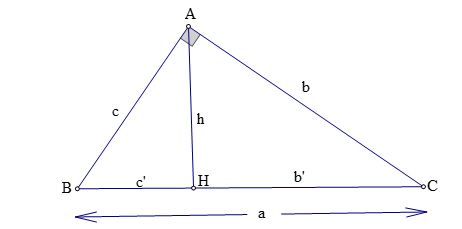
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
Cạnh huyền nhân cùng với sin góc đối xuất xắc nhân cùng với côsin góc kề.Cạnh góc vuông cơ nhân với chảy của góc đối giỏi nhân với cotg của góc kề.b = a.sin
B = a.cos
C; c = a.sin
C = a.cos
B; b = c.tan
B = c.cot
C; c = b.tan
C = b.cot
C
Chú ý: vào một tam giác vuông nếu đến trước hai yếu tố (trong kia có tối thiểu một nguyên tố về cạnh cùng không nhắc góc vuông) thì ta sẽ tìm kiếm được các nguyên tố còn lại.
Các hệ thức lượng vào tam giác thường
1. Định lý cosin
Định lí: vào một tam giác bất kì, bình phương một cạnh bởi tổng những bình phương của nhì cạnh còn lại trừ đi hai lần tích của nhị cạnh đó nhân với Cosin của góc xen giữa chúng.
Ta có các hệ thức sau:
a² = b² + c² – 2bc.cos
A; (1)
b² = c² + a² – 2ca.cos
B; (2)
c² = a² + b² – 2ab.cos
C. (3)
Hệ quả của định lí cosin:
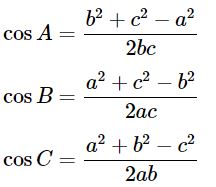
2. Định lí sin
Định lí: vào tam giác ABC bất kỳ, tỉ số giữa một cạnh và sin của góc đối lập với cạnh đó bằng 2 lần bán kính của đường tròn ngoại tiếp tam giác, nghĩa là a⁄sin
A = b⁄sin
B = c⁄sin
C = 2R với R là bán kính đường tròn nước ngoài tiếp tam giác
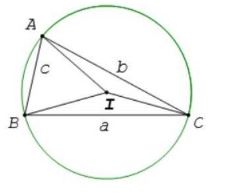
3. Độ dài đường trung tuyến
Cho tam giác ABC có các cạnh BC = a,CA = b cùng AB = c. Gọi ma, mb với mc là độ dài những đường trung tuyến đường lần lượt vẽ từ các đỉnh A, B, C của tam giác. Ta có
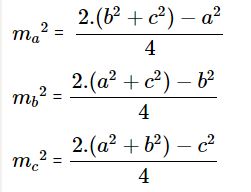
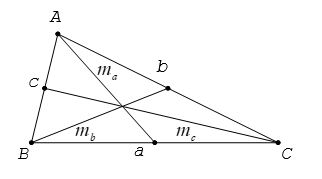
4. Bí quyết tính diện tích tam giác
Diện tích của tam giác ABC được xem theo một trong các công thức sau:
S = ½a.b.sin
C = ½b.c.sin
A = ½c.asin
B (1)
S = abc/4R (2)
S = quảng cáo (3)
S = √p(p-a)(p-b)(p-c) (công thức Hê rông) (4)
Trong đó:
S là diện tích s tam giácR là nửa đường kính đường tròn ngoại tiếp tam giác;r là nửa đường kính đường tròn nội tiếp tam giác;a, b, c là độ dài con đường cao lần lượt tương xứng với những cạnh BC, CA, AB;
Các dạng bài tập hệ thức vào tam giác gồm lời giải
Dạng 1: thống kê giám sát các đại lượng.
Phương pháp giải: Vận dụng các định lí sin, cosin, trung tuyến, diện tích s và tình dục giữa các đại lượng bắt buộc tính, những dạng tam giác sệt biệt.
Ví dụ 1: cho tam giác ABC gồm AB = 1cm , AC = 2cm với Aˆ = 120° . Tính BC
Lời giải
Áp dụng định lí cosin ta có:
BC² = AB² + AC² – 2AB.AC.cos Aˆ
BC² = 1² + 2² – 2.1.2.cos120°
BC² = 1 + 4 – 4.(-½) = 7
BC = √7 cm
Ví dụ 2: đến tam giác ABC vuông tại A. Biết cos B = 0,8. Hãy tính các tỉ số lượng giác của góc C.
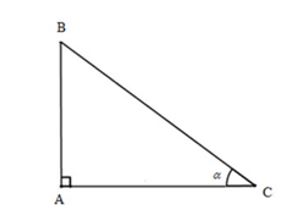
Lời giải
Xét tam giác ABC vuông trên A gồm Aˆ = 90°Bˆ + Cˆ = 90°
Do kia Bˆ và Cˆ là nhì góc phụ nhau
⇒ sin
C = cos
B = 0,8
Từ công dụng bài 14 ta có:
sin2C + cos2C = 1
⇔ cos2C = 1 – sin2C
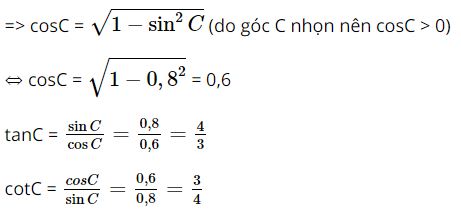
Vậy sin
C = 0,8; cos
C = 0,6; tan
C = 4⁄3;cot
C = ¾
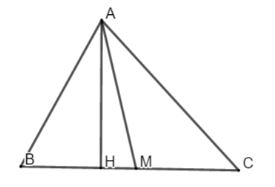
Ví dụ 3: mang lại tam giác vuông tất cả một góc 60° và cạnh huyền bao gồm độ lâu năm là 8. Hãy tìm kiếm độ nhiều năm của cạnh đối lập với góc 60°.
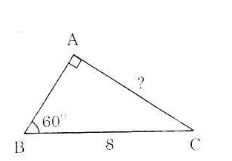
Giả sử ta tất cả tam giác ABC như bên trên hình. Ta có:
sin
B = AC/BC
⇒AC = BC.sin
B = 8.sin60° = 4√3
Dạng 2: chứng tỏ hệ thức, tính giá trị các biểu thức
Phương pháp giải: vận dụng các phương pháp chứng minh đẳng thức: chuyển đổi sao mang đến hai vế bằng nhau, từ giả thiết lúc đầu dẫn cho một đẳng thức vẫn được thừa nhận là đúng,… Sử dụng những định lí vào tam giác vuông, tam giác thường, các hệ thức lượng vào tam giác.
Ví dụ 1: mang lại hình bình hành ABCD, chứng tỏ rằng BD² + AC² = 2(AB² + AD²)
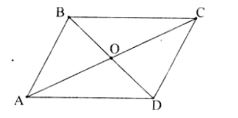
Lời giải
Ta tất cả O là trọng điểm hình bình hành ABCD ⇒ O là trung điểm của AC.
BO là trung đường của tam giác ABC ứng cùng với cạnh AC.
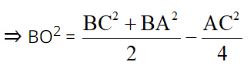
4BO² = 2(BC² + BA²) – AC² (1)
Mà O là trung điểm của BD ⇒ BD = 2BO ⇒ BD² = 4BO² (1)
⇒ BD² = 2(CB² + AB²) – AC²
⇒ BD² + AC² = 2(CB² + AB²)
⇒ BD² + AC² = 2(AB² + AD²) ( bởi AD = CB ) (điều rất cần được chứng minh)
Ví dụ 2: minh chứng rằng giá bán trị của các biểu thức sau không phụ thuộc vào số đo của góc nhọn α:
a) A = cos4α + 2cos²αsin²α + sin4α
b) B = sin4α + cos²α.sin²α + cos²α
Lời giải
a) A = cos4α + 2cos²αsin²α + sin4α
= (cos²α)² + 2cos²αsin²α + (sin²α)²
= (cos²α + sin²α)² (do sin²α + cos²α = 1)
= 1
b) B = sin4α + cos²α.sin²α + cos²α
= (sin4α + cos²α . Sin²α) + cos²α
= sin²α . (sin²α + cos²α) + cos²α (do sin²α + cos²α = 1)
sin²α . 1 + cos²α = 1
Ví dụ 3: chứng tỏ định lý sin: vào tam giác nhọn, độ dài những cạnh tỉ lệ thành phần với sin của những góc đối diện a/sin
A = b/sin
B = c/sin
C
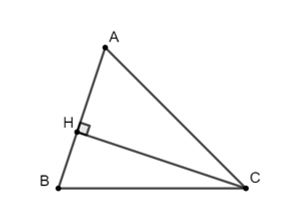
Lời giải
Vẽ mặt đường cao CH
Xét ΔAHC vuông tại H có: sin
A = CH/AC
Xét ΔAHB vuông tại H có: sin
B = CH/BC
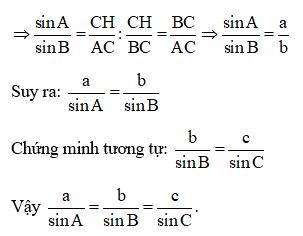
Dạng 3: chứng tỏ tam giác.
Phương pháp giải: Áp dụng những hệ thức lượng vào tam giác, những định lí, công thức về diện tích, đường trung đường và những bất đẳng thức, hằng đẳng thức cơ bản.
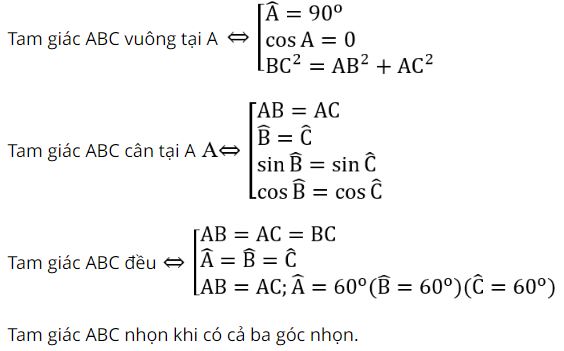
Ví dụ 1: cho tam giác ABC. Chứng tỏ Aˆ nhọn khi và chỉ còn khi BC² 90° ⇒ cos
Aˆ > 0
⇒ AB² + AC²- BC² > 0
⇒ BC² Dạng 4: Giải tam giác và những bài toán thực tế. Xem thêm: Cách Để Viết Nhật Ký Công Việc Hàng Ngày 2022, Top 28 Mẫu Sổ Ghi Chép Công Việc Hàng Ngày 2022
Phương pháp giải: Giải tam giác là tìm kiếm số đo các cạnh, những góc còn lại trong tam giác lúc biết những giải thiết, áp dụng những hệ thức lượng, định lí, cách làm tính diện tích, mặt đường trung tuyến,… bài xích toán thực tế được giải bằng phương pháp chuyển về việc tam giác để xác minh số đo được yêu cầu.
Ví dụ 1. Cho ΔABC tất cả AB = 12, BC = 15, AC = 13
a. Tính số đo các góc của ΔABC
b. Tính độ dài các đường trung con đường của ΔABC
c. Tính diện tích s tam giác ABC, nửa đường kính đường tròn nội tiếp, bán kính đường tròn ngoại tiếp tam giác ABC
d. Tính độ dài con đường cao nối từ các đỉnh của tam giác ABC
Lời giải
a. Áp dụng hệ thức lượng trong tam giác ta có:
AB² = AC² + BC² – 2AC.BC.cos
ACBˆ
⇔ 12² = 13² + 15² – 2.13.15.cos
ACBˆ
⇔ cos
ACBˆ = 25⁄39 ⇒ ACBˆ ≈50°7′

c. Để tính được diện tích s một cách đúng chuẩn nhất ta sẽ áp dụng công thức Hê – rông
Nửa chu vi tam giác ABC
p = (AB + AC + BC) : 2 = (12+13+15):2 = 20
Diện tích tam giác ABC:
S = √p(p-AB)(p-AC)(p-BC) = 20√14
Bán kính mặt đường tròn nước ngoài tiếp R của tam giác ABC:

Sau khi gọi xong nội dung bài viết của chúng tôi có thể giúp các bạn củng chũm lại các kiến thức về hệ thức lượng trong tam giác vuông, cân, thường để áp dụng vào làm bài xích tập nhé
Trong bài viết dưới đây, chúng tôi sẽ kể lại các kiến thức về hệ thức lượng trong tam giác vuông, cân, thường giúp các bạn củng nạm lại kỹ năng và kiến thức vận dụng giải bài bác tập tiện lợi nhé
Các hệ thức lượng vào tam giác
1. Định lý Cosin
Trong một tam giác bất kì, bình phương một cạnh bởi tổng các bình phương của nhị cạnh còn sót lại trừ đi nhị lần tích của nhị cạnh đó nhân cùng với cosin của góc xen thân chúng.
a2 = b2 + c2 – 2bc.cosA;b2 = c2 + a2 – 2ca.cos
B;c2 = a2 + b2 – 2ab.cos
C.
Hệ quả:
Cos A = (b2 + c2 – a2)/2bcCos B = (a2 + c2 – b2)/2ac
Cos C = (a2 + b2 – c2)/2ab
2. Định lý Sin
Trong tam giác ABC bất kỳ, tỉ số giữa một cạnh và sin của góc đối lập với cạnh kia bằng 2 lần bán kính của mặt đường tròn nước ngoài tiếp tam giác. Ta có:
a /sin
A = b/sin
B = c/sin
C = 2R
Với R là bán kính đường tròn nước ngoài tiếp tam giác
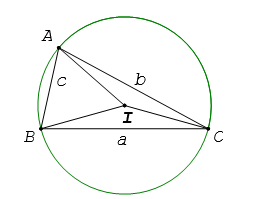
Ngoài ra, các bạn nên đọc thêm công thức lượng giác cụ thể tại đây.
3. Độ dài mặt đường trung tuyến đường của tam giác
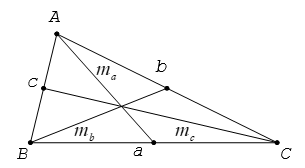
Cho tam giác ABC tất cả độ nhiều năm cạnh BC = a, CA = b, AB = c. Gọi ma, mb, mc theo thứ tự là độ dài các đường trung con đường vẽ từ đỉnh A, B, C của tam giác.Ta có
ma2 = <2(b2 + c2) – a2>/4mb2 = <2(a2 + c2) – b2>/4mc2 = <2(a2 + b2) – c2>/44. Phương pháp tính diện tích tam giác
Ta kí hiệu ha, hb và hc là các đường cao của tam giác ABClần lượt vẽ từ những đỉnh A, B, C với S là diện tích tam giác đó.
Diện tích S của tam giác ABC được xem theo một trong số công thức sau:
S = ½absinC = ½bcsin
A = ½casin
BS = abc/4RS = pr
S = √p(p – a)(p – b)(p – c) (công thức hê – rông)
Hệ thức lượng vào tam giác vuông
1. Các hệ thức về cạnh và mặt đường cao trong tam giác vuông
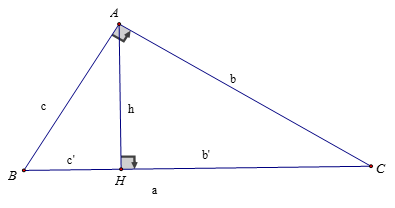
Cho ΔABC, góc A bằng 900, AH ⊥ BC, AB = c, AC = b, BC = a, AH = h thì:
BH = c’ được call là hình chiếu của AB xuống BCCH = b’ được hotline là hình chiếu của AC xuống BCKhi đó, ta có:
c2 = a.c’ (AB2 = BH.BC) b2 = a.b’ (AC2 = CH.BC)h2 = b’.c’ (AH2 = CH.BH)b.c = a.h (AB.AC = AH.BC )1/h2 = 1/b2 + 1/c2 (1/AH2 = 1/AB2 + 1/AC2)b2 + c2 = a2 (AB2 + AC2 = BC2)(Định lý Pytago)2. Tỉ con số giác của góc nhọn
a. Định nghĩa
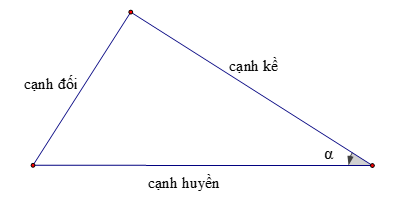
b. Định lí
Nếu nhị góc phụ nhau thì sin góc này bằng cosin góc kia, tang góc này bởi cotang góc kia.
c. Một số hệ thức cơ bản
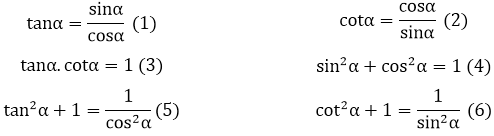
d. So sánh những tỉ con số giác
Cho góc nhọn α, ta có:
a) mang đến α,β là nhị góc nhọn. Nếu như α sinα cosα > cosβ; cotα > cotβ
b) sinα 2. Hệ thức về góc và cạnh trong tam giác vuông
a. Các hệ thức
Trong một tam giác vuông, từng cạnh góc vuông bằng:
Cạnh huyền nhân với sin góc đối hoặc nhân với cos góc kềCạnh góc vuông tê nhân với tan góc đối hoặc cot góc kề
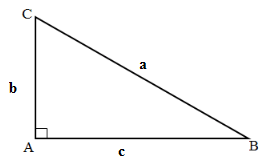
B = a.cos
Cc = a.sin
C = a.cos
Bb = c.tan
B = c.cot
Cc = b.tan
B = b.cot
C
3. Giải tam giác và ứng dụng vào vấn đề đo đạc
Giải tam giác : Giải tam giác là tìm một vài yếu tố của tam giác khi đã biết những yếu tố không giống của tam giác đó.
Muốn giải tam giác ta buộc phải tìm mối contact giữa những yếu tố đã cho với các yếu tố không biết của tam giác thông qua các hệ thức đã làm được nêu vào định lí cosin, định lí sin và các công thức tính diện tích s tam giác.
Các câu hỏi về giải tam giác:
Có 3 vấn đề cơ phiên bản về gỉải tam giác:
a) Giải tam giác lúc biết một cạnh với hai góc.
Đối với bài toán này ta thực hiện định lí sin để tính cạnh còn lại
b) Giải tam giác lúc biết hai cạnh cùng góc xen giữa
Đối với việc này ta thực hiện định lí cosin nhằm tính cạnh sản phẩm ba
c) Giải tam giác lúc biết ba cạnh
Đối với việc này ta áp dụng định lí cosin nhằm tính góc
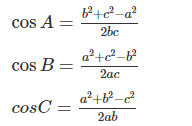
Lưu ý:
Cần để ý là một tam giác giải được khi ta biết 3 yếu tố của nó, trong đó phải có ít nhất một nhân tố độ nhiều năm (tức là yếu tố góc không được thừa 2)Việc giải tam giác được sử dụng vào các bài toán thực tế, nhất là các bài toán đo đạc.Các dạng bài xích tập về hệ thức lượng vào tam giác vuông, cân nặng và thường
Ví dụ 1: mong tính khoảng cách từ điểm A tới điểm B nằm cạnh kia trườn sông, ông Việt vun từ A mặt đường vuông góc với AB. Trê tuyến phố vuông góc này lấy một đoạn thằng A C=30 m, rồi vun CD vuông góc cùng với phương BC giảm AB trên D (xem hình vẽ). Đo được AD = 20m, từ đó ông Việt tính được khoảng cách từ A đến B. Em hãy tính độ dài AB và số đo góc ACB.
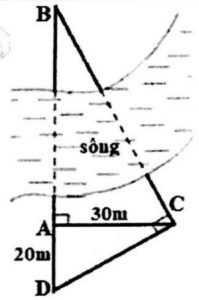
Lời giải:
Xét Δ BCD vuông tại C cùng CA là đường cao, ta có:
AB.AD = AC2 (hệ thức lượng)

Vậy tính độ nhiều năm AB = 45 m cùng số đo góc ngân hàng á châu acb là 56018′
Ví dụ 2: mang đến ΔABC gồm AB = 12, BC = 15, AC = 13
a. Tính số đo những góc của ΔABC
b. Tính độ dài các đường trung con đường của ΔABC
c. Tính diện tích s tam giác ABC, nửa đường kính đường tròn nội tiếp, bán kính đường tròn ngoại tiếp tam giác ABC
d. Tính độ dài con đường cao nối từ các đỉnh của tam giác ABC
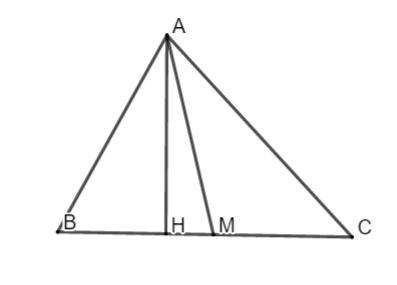
Lời giải:
a. Áp dụng hệ thức lượng trong tam giác ta có:

c. Để tính được diện tích s một cách chính xác nhất ta sẽ áp dụng công thức Hê – rông



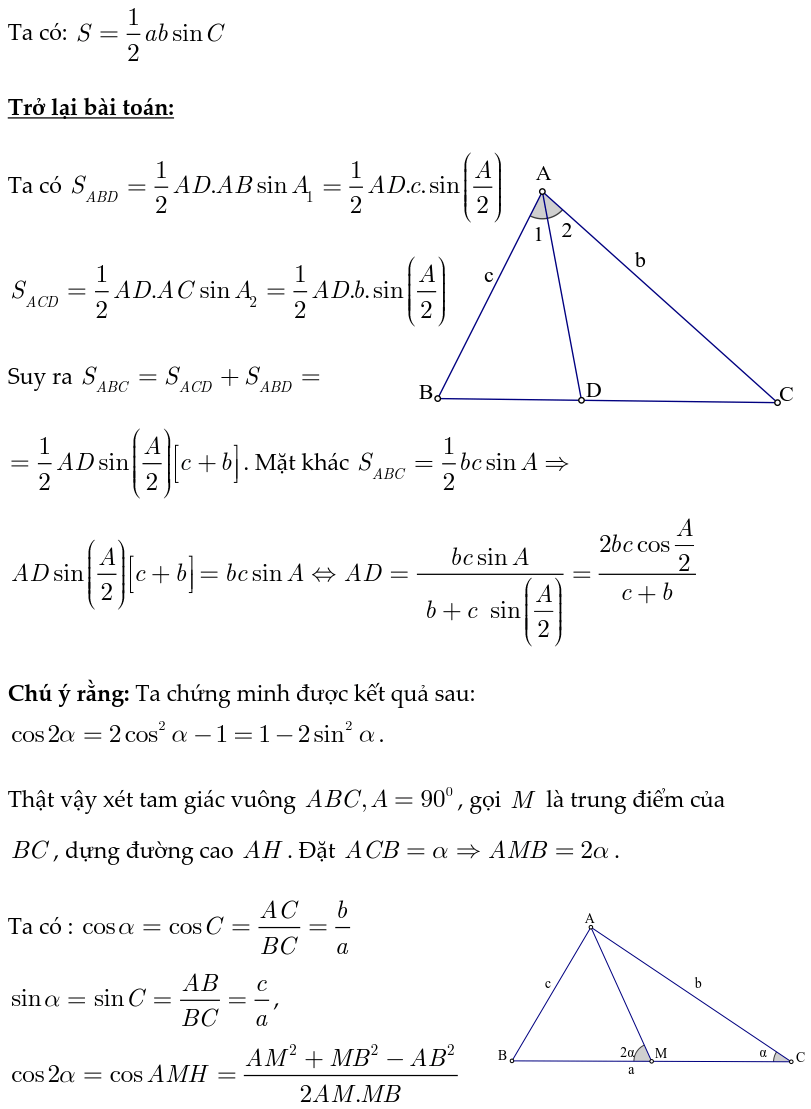
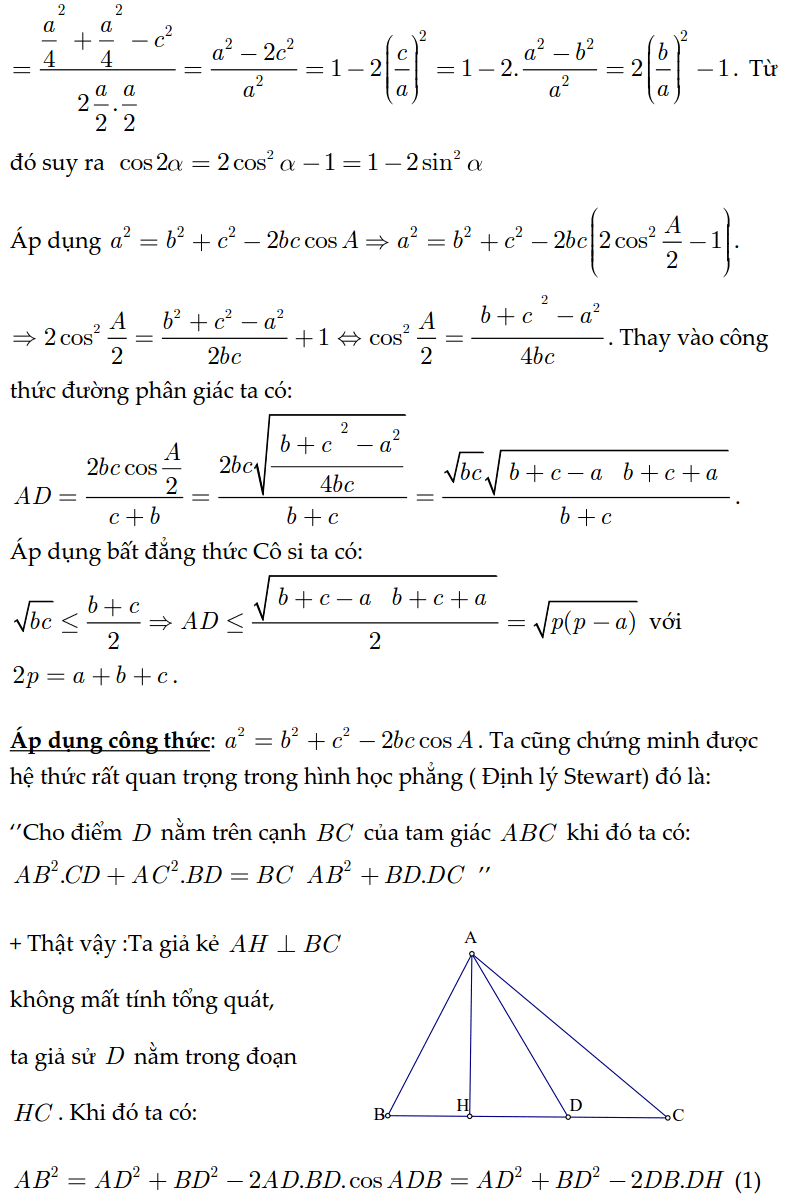

Ví dụ 4: Một bạn thợ áp dụng thước ngắm gồm góc vuông đề đo độ cao của một cây dừa, cùng với các form size đo được như hình bên. Khoảng cách từ vị trí cội cây mang lại vị trí chân của tín đồ thợ là 4,8m và từ địa điểm chân đứng thẳng xung quanh đất mang lại mắt của fan ngắm là l,6m. Hỏi cùng với các form size trên thì fan thợ đo được chiều cao của cây đó là bao nhiêu? (làm tròn đến mét).
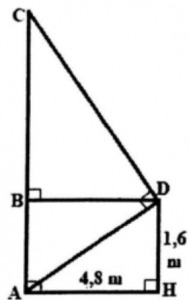
Lời giải:
Xét tứ giác ABDH có
Xét tứ giác ABDH có:

Vậy chiều cao của cây dừa là 16 m.
Ví dụ 5: cho tam giác ABC vuông tại A, con đường cao AH .
a. Biết AH = 6cm, bh = 4,5cm, Tính AB, AC, BC,HCb. Biết AB = 6cm, bh = 3cm, Tính AH, AC, CH
Lời giải:
a. Áp dụng định lý Pi-Ta-Go mang lại tam giác vuông AHB vuông trên H
Ta có: AB2 = AH2 + BH2 = 62+ 4,52= 56,25 cm2
Suy ra: AB √56,25 = 7,5( cm)
Áp dụng hệ thức lượng trong tam giác vuông ABC vuông trên A, AH là độ cao ta được:
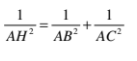

b. Trong tam giác vuông ABH vuông tại H.
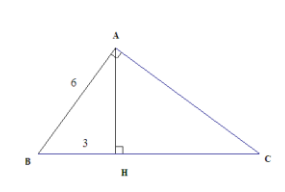
Ta có: AB2 = AH2 + BH2
=> AH2 = AB2 – BH2 = 62 – 32 = 27
Vậy AH = √27 = 5,2cm

Hy vọng cùng với những kỹ năng và kiến thức về hệ thức lượng trong tam giác mà chúng tôi vừa phân tích kỹ phía trên có thể giúp bạn nắm chắc được công thức để áp dụng giải những bài tập.








