
Đầy đầy đủ lý thuyết, bài bác tập về chứng tỏ ba điểm thẳng mặt hàng hình học lớp 7 có giải mã
mua xuống 11 14.922 164
Tailieumoi.vn xin ra mắt đến các quý thầy cô, những em học sinh đang trong quá trình ôn tập bộ bài xích tập chứng minh ba điểm thẳng mặt hàng hình học tập lớp 7, tài liệu bao hàm 11 trang, tuyển chọn chọn bài bác tập minh chứng ba điểm thẳng hàng hình họcđầy đầy đủ lý thuyết, phương thức giải cụ thể và bài xích tập có đáp án (có lời giải), giúp các em học viên có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kỹ năng và sẵn sàng cho kì thi môn Toán sắp tới tới. Chúc những em học viên ôn tập thật tác dụng và đạt được kết quả như ao ước đợi.
Bạn đang xem: Cách chứng minh 3 điểm thẳng hàng lớp 7
Tài liệu minh chứng ba điểm thẳng hàng hình học tập lớp 7 gồm những nội dung bao gồm sau:
A. Phương thức giải
- tóm tắt kim chỉ nan ngắn gọn.
B. Một số ví dụ
- gồm 6 ví dụ minh họa đa dạng của các dạng bài tập minh chứng ba điểm thẳng hàng hình học tập lớp 7 có giải thuật chi tiết.
C. Bài tập vận dụng
- tất cả 9 bài xích tập áp dụng có câu trả lời và lời giải cụ thể giúp học viên tự rèn luyện bí quyết giải các dạng bài bác tập chứng tỏ ba điểm thẳng sản phẩm hình học tập lớp 7.
Mời các quý thầy cô và các em học viên cùng xem thêm và mua về cụ thể tài liệu bên dưới đây:
CHỨNG MINH tía ĐIỂM THẲNG HÀNG
A. Phương pháp giải
Ba điểm thuộc thuộc một con đường thẳng call là tía điểm trực tiếp hàng. Để chứng tỏ ba điểm trực tiếp hàng, bạn cũng có thể sử dụng một số cách thức sau đây:
1. Cách thức 1.
Nếu ABD^+DBC^=180°thì ba
Điểm A; B; C thẳng hàng.
2. Phương pháp 2.
Nếu AB // a cùng AC // a thì ba
điểm A; B; C thẳng hàng.
(Cơ sở của phương pháp này
là: định đề Ơ-Clit)
3. Phương thức 3.
Nếu AB⊥a; AC⊥athì ba
điểm A; B; C trực tiếp hàng.
(Cơ sở của cách thức này
là: Có một và duy nhất đường
thẳng a’ đi qua điểm O và vuông góc với con đường thẳng a đến trước)
Hoặc A; B; C thuộc thuộc một con đường trung trực của một quãng thẳng.
4. Phương pháp 4.
Nếu tia OA và tia OB là hai tia phân giác của góc x
Oy thì ba điếm O; A; B trực tiếp hàng.
(Cơ sở của cách thức này là:
Mỗi góc không giống góc bẹt tất cả một và duy nhất tia phân giác).
* Hoặc: nhị tia OA và OB cùng nằm trên nửa phương diện phẳng bờ chứa
tia Ox, x
OA^=x
OB^thì tía điểm O, A, B trực tiếp hàng.
5. trường hợp K là trung điểm BD, K’ là giao điểm của BD với AC. Ví như K’ là trung điểm BD thì K"≡Kvà A, K, C thẳng hàng.
(Cơ sở của cách thức này là: từng đoạn thẳng chỉ có một trung điểm).
B. Một vài ví dụ
Ví dụ 1. cho tam giác ABC vuông ngơi nghỉ A, M là trung điểm AC. Kẻ tia Cx vuông góc CA (tia Cx với điểm B ở hai nửa mặt phẳng đối nhau bờ AC).Trên tia Cx lấy điểm D làm sao cho CD = AB. Minh chứng ba điểm B, M, D trực tiếp hàng.
Giải
* Tìm giải pháp giải. mong mỏi B, M, D thẳng hàng
cần hội chứng minh
BMC^+CMD^=180°. Do
AMB^+BMC^=180°
nên yêu cầu chứng minh
AMB^=DMC^
* Trình bày lời giải
ΔAMB vàΔCMD có:
AB = DC (gt),BAM^=DCM^=90°,
MA = MC (M là trung điểm AC)
Do đó: ΔAMB=ΔCMD (c.g.c), suy ra:AMB^=DMC^
Mà AMB^+BMC^=180° (kề bù) nên
BMC^+CMD^=180°
Vậy bố điểm B; M; D thẳng hàng.
Ví dụ 2. mang đến hai đoạn thẳng AC và BD giảm nhau trên trung điểm O của mỗi đoạn. Bên trên tia AB rước điểm M làm thế nào cho B là trung điểm AM, bên trên tia AD mang điểm N làm thế nào cho D là trung điểm AN. Minh chứng ba điểm M, C, N trực tiếp hàng.
Giải
* Tìm cách giải. bệnh minh: cm // BD và công nhân // BD từ kia suy ra M, C, N thẳng hàng.
Thaygiaongheo.com hướng dẫn các em học sinh lớp 7 một số biện pháp chứng minh 3 điểm thẳng sản phẩm trong chương trình Toán lớp 7.
Trong chương trình Toán lớp 6 ở phần Hình học các em đã biết thế nào là 3 điểm thẳng hàng. Và chứng minh 3 điểm thẳng hàng trong Hình học lớp 7 như nào?
Cách chứng minh 3 điểm thẳng sản phẩm ở lớp 7
Để chứng minh 3 điểm thẳng sản phẩm ở lớp 7 họ thường áp dụng những bí quyết sau:
Nếu 3 điểm thuộc tạo với nhau thành 1 góc bằng 180° thì 3 điểm đó thẳng sản phẩm (đã học ở lớp 6).Qua một điểm chỉ kẻ được duy nhất một đường thẳng tuy nhiên song (hoặc vuông góc) với đường thẳng mang đến trước.Chứng minh 3 điểm cùng nằm trên một đường thẳng (đường cao, đường trung tuyến, đường phân giác).Bài tập chứng minh 3 điểm thẳng hàng gồm lời giải
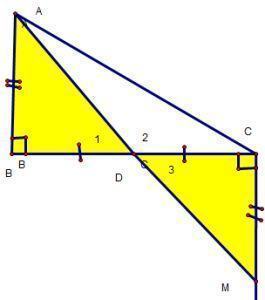
Bài 1: cho ΔABC vuông tại B. Trên nữa mặt phẳng bờ BC không tồn tại điểm A, vẽ tia Cx vuông góc BC. Bên trên tia Cx lấy M thế nào cho CM = AB. Chứng minh A, M với D là trung điểm của BC thẳng hàng.
Giải. Xem thêm: Trên Tay Và Đánh Giá Chi Tiết Samsung Galaxy S6 Edge, Có Nên Mua?
Xét ΔABD cùng ΔMCD, ta tất cả :

Mặt khác :
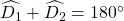
&r
Arr;
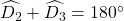
Hay :
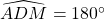
&r
Arr; A, D, M thẳng mặt hàng ( góc bẹt) Nhận xét: Ở bài này chứng minh 3 điểm thẳng mặt hàng bằng biện pháp chứng minh mang đến góc tạo bởi 3 điểm bằng 180°.
Bài 2: mang lại tam giác ABC . Gọi D, E lần lượt là trung điểm của AB, AC. Bên trên tia đối của tia DC, lấy điểm M làm thế nào để cho MD = CD. Trên tia đối của tia EB, lấy điểm N thế nào cho EN = BE. Chứng minh : A là trung điểm của MN.
GIẢI.
Xét ΔBCD cùng ΔBMD, ta bao gồm :
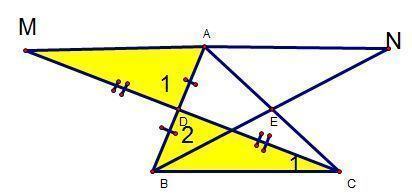
DB = domain authority (D là trung điểm của AB)
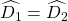
DC = DM (gt).
&r
Arr; ΔBCD = ΔBMD (c -g -c)
&r
Arr;
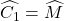
Mà :
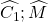
Chứng minh tương tự, ta được : BC // AN và BC = AN.
Ta gồm : BC // AM (cmt) cùng BC // AN (cmt)
&r
Arr; A, M, N thẳng hàng. (1)
BC = AM và BC = AN => AM = AN (2).
Từ (1) với (2), suy ra : A là trung điểm của MN.
Nhận xét:Chứng minh 3 điểm A, M, N thẳng sản phẩm trước, sau đó chứng minh AM= AN
Bài 3: đến tam giác ABC vuông góc tại A gồm góc B = 53°.
a) Tính góc C.
b) bên trên cạnh BC, lấy điểm D sao cho BD = BA. Tia phân giác của góc B cắt cạnh AC ở điểm E. Chứng minh rằng : ΔBEA = ΔBED.
c) Qua C, vẽ đường thẳng vuông góc với BE tại H. CH cắt đường thẳng AB tại F. Cm : ΔBHF = ΔBHC.
d) Chứng minh rằng : ΔBAC = ΔBDF cùng 3 điểm D, E, F thẳng hàng.
Giải.
a. Tính góc C
Xét ΔBAC, ta có :
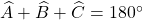
&r
Arr;
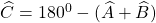
&r
Arr;
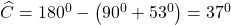
b. ΔBEA = ΔBED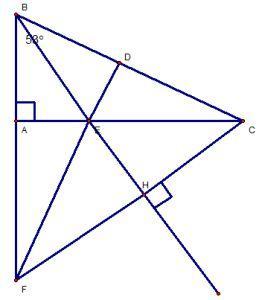
Xét ΔBEA với ΔBED, ta có :
BE cạnh chung.
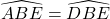
BD = bố (gt)
&r
Arr; ΔBEA = ΔBED (c – g – c)
c. ΔBHF = ΔBHC
Xét ΔBHF với ΔBHC, ta bao gồm :
BH cạnh chung.
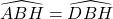
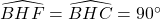
&r
Arr; ΔBHF = ΔBHC (cạnh huyền – góc nhọn)
&r
Arr; BF = BC (cạnh tương ứng)
d. ΔBAC= ΔBDF cùng D, E, F thẳng hàng
Xét ΔBAC cùng ΔBDF, ta có:
BC = BF (cmt)
Góc B chung.
BA = BC (gt)
&r
Arr; ΔBAC = ΔBDF
&r
Arr;
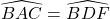
Mà :
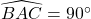
Nên :
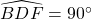
Mặt khác :
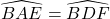
Mà :
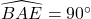
Nên :
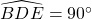
Từ (1) cùng (2), suy ra : DE trùng với DF
Hay 3 điểm D, E, F thẳng hàng.
Bài tập về nhà
Bài 1: đến tam giác ABC. Trên tia đối của tia AB lấy điểm F làm thế nào để cho AB = FA. Trên tia đối của tia AC lấy điểm E sao để cho AC = AE.
a) Chứng minh: ΔEAF = ΔCAB
b) Gọi K là trung điểm EF với D là trung điểm BC. Chứng minh : KB = FD.
d) Chứng minh: K, A, D thẳng hàng.
Bài 2: Cho Δ ABC gồm M là trung điểm của AB. Trên tia đối của tia MC lấy điểm D làm thế nào cho MD = MC.
a) Chứng minh ΔMAD = ΔMBC cùng AD // CB.
b) Lấy N thuộc AD; NM cắt BC tại phường Chứng minh AN = BP.
c) trên nửa mặt phẳng bờ AB ko chứa điểm D, vẽ tia AE làm sao cho góc EAB + góc ABC = 180°.








