Với Công thức tìm tọa độ giao điểm của hai đường thẳng hay, chi tiết Toán lớp 9 chi tiết nhất giúp học sinh dễ dàng nhớ toàn bộ các Công thức tìm tọa độ giao điểm của hai đường thẳng từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:
Công thức tìm tọa độ giao điểm của hai đường thẳng hay, chi tiết - Toán lớp 9
I. Lý thuyết
+ Cho hai đường thẳng d: y = ax + b và d’: y = a’x + b’ với a ≠0 và a’ ≠0 .
Bạn đang xem: Tìm giao điểm của 2 đường thẳng
Hai đường thẳng này có duy nhất một điểm chung khi chúng cắt nhau.
Hai đường thẳng không có điểm chung khi chúng song song.
Hai đường thẳng có vô số điểm chung khi chúng trùng nhau.
+ Muốn tìm tọa độ giao điểm hai đường thẳng ta làm như sau (d và d’ cắt nhau)
Bước 1: Xét phương trình hoành độ giao điểm của d và d’.
ax + b = a’x + b’ (1)
Chú ý:
+ Phương trình (1) vô nghiệm thì d // d’.
+ Phương trình (1) luôn đúng với mọi giá trị x thì d và d’ trùng nhau.
+ Với a ≠ a’, phương trình (1) có nghiệm duy nhất.
(1)⇔ax−a"x=−b+b"
⇔xa−a"=−b+b"
⇔x=−b+b"a−a"
Ta chuyển qua bước 2
Bước 2: Thay x vừa tìm được vào d hoặc d’ để tính y
Ví dụ thay x vào d⇒y=a.−b+b"a−a"+b
Bước 3: Kết luận tọa độ giao điểm.
II. Các ví dụ
Ví dụ 1: Tìm tọa độ giao điểm của các đường thẳng sau:
a) d: y = 3x – 2 và d’: y = 2x + 1;
b) d: y = 4x – 3 và d’: y = 2x + 1.
Lời giải:
a) Phương trình hoành độ giao điểm của d và d’ là:
3x – 2 = 2x + 1
⇔3x−2x=1+2
⇔x=3
Thay x = 3 và d ta được:
y=3.3−2=9−2=7
Vậy tọa độ giao điểm của d và d’ là A(3; 7).
b) Phương trình hoành độ giao điểm của d và d’ là:
4x – 3 = 2x + 1
⇔4x−2x=3+1
⇔2x=4
⇔x=2
Thay x vào d ta được:y=4.2−3=5
Vậy tọa độ giao điểm của d và d’ là B(2; 5).
Ví dụ 2: Tìm tham số m để:
a) d: y = 2mx + 5 và d’: y = 4x + m cắt nhau tại điểm có hoành độ bằng 1.
b) d: y = (3m – 2)x – 4 cắt trục hoành tại điểm có hoành độ bằng 3.
Lời giải:
a) Phương trình hoành độ giao điểm của d và d’ là:
2mx + 5 = 4x + m.
Vì hai đường thẳng d và d’ cắt nhau tại điểm có hoành độ bằng 1 nên thay x = 1 vào phương trình hoành độ giao điểm ta có:
2m.1 + 5 = 4.1 + m
⇔2m+5=4+m
⇔2m−m=4−5
⇔m=−1
Vậy m = -1 thì d và d’ cắt nhau tại điểm có hoành độ bằng 1.
b) Vì d cắt trục hoành tại điểm có hoành độ bằng 3 nên giao điểm của d với trục hoành là A(3; 0). Thay tọa độ điểm A vào d ta được:
Giao điểm của 2 đường thẳng là một phần kiến thức cơ bản trong chương trình Toán 6. Vậy giao điểm là gì? Cách xác định giao điểm của 2 đường thẳng như thế nào? Cùng tìm hiểu qua bài viết sau đây.
Trong thực tế, ta bắt gặp rất nhiều hình ảnh về giao điểm. Vậy giao điểm là gì? Và làm thế nào để xác định giao điểm của 2 đường thẳng? Bài viết dưới đây sẽ trình bày chi tiết cho các em một số kiến thức trọng tâm như khái niệm và cách xác định giao điểm của hai đường thẳng, cùng với đó là các dạng bài tập hay và thú vị, thôi thúc niềm đam mê Toán học của các em.
1. Giao điểm là gì?
Hai đường thẳng cắt nhau là hai đường thẳng chỉ có một điểm chung và điểm chung này được gọi là giao điểm của hai đường thẳng đó.
Cách phát biểu khác: Giao điểm của hai đường thẳng là điểm chung duy nhất của hai đường thẳng đó.
Ví dụ 1. Em hãy chỉ ra các giao điểm của các cặp đường thẳng cắt nhau được minh họa bời hình sau:
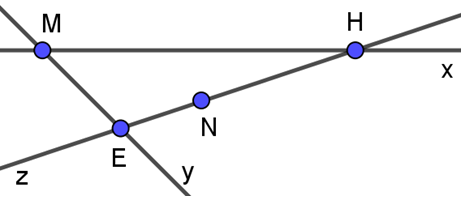
Lời giải
Các giao điểm của các cặp đường thẳng cắt nhau trong hình trên là:
+ Giao điểm của đường thẳng x và đường thẳng y là điểm M.
+ Giao điểm của đường thẳng x và đường thẳng z là điểm H.
+ Giao điểm của đường thẳng z và đường thẳng y là điểm E.
2. Các dạng toán về giao điểm của 2 đường thẳng
2.1. Dạng 1: Bài toán tìm giao điểm của 2 đường thẳng
*Phương pháp giải: Muốn tìm giao điểm của hai đường thẳng, ta xác định một điểm chung duy nhất của hai đường thẳng đó, khi đó điểm chung tìm được chính là giao điểm mà ta cần tìm.
Bài tập vận dụng:
Em hãy quan sát hình vẽ dưới đây và chỉ ra các giao điểm của các cặp đường thẳng cắt nhau đó.
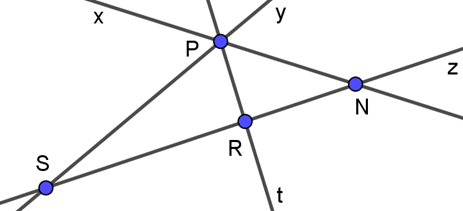
Các giao điểm của các cặp đường thẳng cắt nhau trong hình trên là:
+ Giao điểm của đường thẳng x và đường thẳng y là điểm P.
+ Giao điểm của đường thẳng x và đường thẳng z là điểm N.
Xem thêm: Xem Hương Mật Tựa Khói Sương ' Sau 5 Năm, Hương Mật Tựa Khói Sương
+ Giao điểm của đường thẳng x và đường thẳng t là điểm P.
+ Giao điểm của đường thẳng y và đường thẳng z là điểm S.
+ Giao điểm của đường thẳng y và đường thẳng t là điểm P.
+ Giao điểm của đường thẳng z và đường thẳng t là điểm R.
2.2. Dạng 2: Bài tập tính số giao điểm
Cho bài toán sau: Cho n (n > 1) đường thẳng, biết hai đường thẳng bất kỳ nào trong n đường thẳng đó luôn cắt nhau tại một điểm và không có ba đường thẳng nào cùng có một điểm chung. Hãy tính số giao điểm của chúng.
*Phương pháp giải:
+ Ta chọn ra 1 đường thẳng trong n đường thẳng đã cho, khi đó đường thẳng này sẽ cắt n – 1 đường thẳng còn lại và số giao điểm được tạo ra là: n – 1 (giao điểm);
+ Vì có n đường thẳng nên số giao điểm được tạo ra là: n . (n – 1) (giao điểm);
+ Số giao điểm bị lặp lại 2 lần nên số giao điểm thực tế là: n . (n – 1) : 2 (giao điểm).
Đáp số: Số giao điểm cần tính là n . (n – 1) : 2 giao điểm.
Ví dụ 2. Cho 10 đường thẳng, biết hai đường thẳng bất kỳ nào trong 10 đường thẳng đó luôn cắt nhau tại một điểm và không có ba đường thẳng nào cùng có một điểm chung. Hãy tính số giao điểm của chúng.
Lời giải
+ Ta chọn ra 1 đường thẳng trong 10 đường thẳng đã cho, khi đó đường thẳng này sẽ cắt 9 đường thẳng còn lại và số giao điểm được tạo ra là: 9 (giao điểm);
+ Vì có 10 đường thẳng nên số giao điểm được tạo ra là: 10 . 9 = 90 (giao điểm);
+ Số giao điểm bị lặp lại 2 lần nên số giao điểm thực tế là: 90 : 2 = 45 (giao điểm).
Đáp số: Số giao điểm cần tính là 45 giao điểm.
Bài tập vận dụng:
Cho 32 đường thẳng, biết hai đường thẳng bất kỳ nào trong 32 đường thẳng đó luôn cắt nhau tại một điểm và không có ba đường thẳng nào cùng có một điểm chung. Hãy tính số giao điểm của chúng.
ĐÁP ÁN+ Ta chọn ra 1 đường thẳng trong 32 đường thẳng đã cho, khi đó đường thẳng này sẽ cắt 31 đường thẳng còn lại và số giao điểm được tạo ra là: 31 (giao điểm);
+ Vì có 32 đường thẳng nên số giao điểm được tạo ra là: 32 . 31 = 992 (giao điểm);
+ Số giao điểm bị lặp lại 2 lần nên số giao điểm thực tế là: 992 : 2 = 496 (giao điểm).
Đáp số: Số giao điểm cần tính là 496 giao điểm.
3. Bài tập về giao điểm của 2 đường thẳng
Bài 1. Em hãy quan sát hình vẽ dưới đây và điền câu trả lời thích hợp vào chỗ trống cho các câu sau:
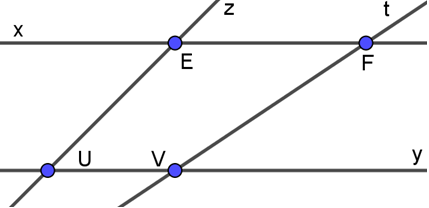
a) Giao điểm của đường thẳng x và đường thẳng t là điểm . . . ;
b) Giao điểm của đường thẳng . . . và đường thẳng . . . là điểm V;
c) Giao điểm của đường thẳng z và đường thẳng y là điểm . . . ;
d) Giao điểm của đường thẳng . . . và đường thẳng . . . là điểm E.
ĐÁP ÁNa) Giao điểm của đường thẳng x và đường thẳng t là điểm F;
b) Giao điểm của đường thẳng t và đường thẳng y là điểm V;
c) Giao điểm của đường thẳng z và đường thẳng y là điểm U;
d) Giao điểm của đường thẳng x và đường thẳng z là điểm E.
Bài 2. Cho ba điểm S, Q, T không thẳng hàng. Em hãy vẽ các đường thẳng SQ, ST và QT và cho biết ba điểm S, Q, T lần lượt là giao điểm của cặp đường thẳng nào.
ĐÁP ÁN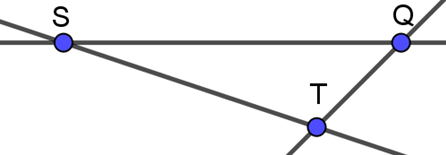
+ Điểm S là giao điểm của đường thẳng SQ và đường thẳng ST;
+ Điểm Q là giao điểm của đường thẳng SQ và đường thẳng QT;
+ Điểm T là giao điểm của đường thẳng ST và đường thẳng QT.
Bài 3. Cho 218 đường thẳng, biết hai đường thẳng bất kỳ nào trong 218 đường thẳng đó luôn cắt nhau tại một điểm và không có ba đường thẳng nào cùng có một điểm chung. Hãy tính số giao điểm của chúng.
ĐÁP ÁN+ Ta chọn ra 1 đường thẳng trong 218 đường thẳng đã cho, khi đó đường thẳng này sẽ cắt 217 đường thẳng còn lại và số giao điểm được tạo ra là: 217 (giao điểm);
+ Vì có 218 đường thẳng nên số giao điểm được tạo ra là: 218 . 217 = 47306 (giao điểm);
+ Số giao điểm bị lặp lại 2 lần nên số giao điểm thực tế là: 47306 : 2 = 23653 (giao điểm).
Đáp số: Số giao điểm cần tính là 23653 giao điểm.
Bài viết trên đây đã trình bày chi tiết cho các em các kiến thức trọng tâm về chuyên đề giao điểm của 2 đường thẳng. Qua đó, hy vọng các em nắm rõ lý thuyết và hoàn thành tốt các dạng bài tập của chuyên đề này.








